密码学笔记
完美保密
完美保密相当于明文密文概率分布独立。
One-Time Pad(OTP)是完美保密。
完美保密要求密钥空间大于等于明文空间(定理5)。
香农定理,明文空间等于密钥空间等于密文空间并且完美保密等价于1.每个密钥等概率被选取,2.任何明文和密文对存在唯一一个密钥作为加密方案的输入。
窃听者不可区分实验。敌手成功区分则实验结果为1。完美保密是实验成功概率严格等于1/2。证明通常可以用规约。
完美保密=完美不可区分性=敌手不可区分性
私钥加密(1)
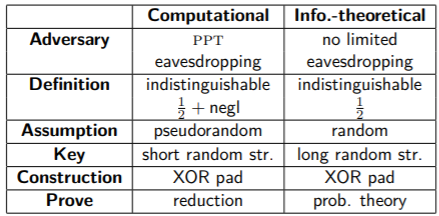
计算安全对比信息论安全。信息论安全就是完美保密。计算安全是只保留能运行可接受时间的敌手和允许敌手以一个非常小的概率成功。
有效的计算是指多项式时间内,可忽略的成功概率是指小于任何多项式的倒数。多项式的参数通常n都是密钥的长度。
私钥加密方案是PPT (Gen,Enc,Dec)。
语义安全。即敌手根据安全参数,外部知识得到任意计算明文的函数有没有密文都是一样的。
窃听者不可区分等价于语义安全。
PRG是一个确定多项式算法,l(n)>n。存在性依赖单向门陷函数的存在性或者P≠NP。
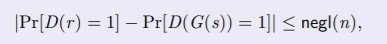
固定长度的加密方案。
A规约到B。
私钥加密(2)
多个加密安全。Enc是确定函数则方案不具有多个加密安全。在多个加密安全实验中使用相同的密钥相当于在窃听者安全实验使用周期性循环的密钥加密明文。
流密码。同步模式和非同步模式。同步模式要求维护流密码。非同步模式要求发送随机初始向量并且要求伪随机生成器能够在初始向量暴露,密钥保密的情况下保持伪随机性。
CPA不可区分性实验。单次加密的CPA安全等于多次加密的CPA安全。变长CPA安全可以被多次加密CPA安全证明。
伪随机函数。

当且仅当伪随机发生器存在,则伪随机函数存在。
CPA安全加密。规约证明。

在CPA安全加密方案中需要真随机函数的范围。

伪随机置换和强伪随机置换,区别在于是否允许使用逆置换预言机。
电子密码本(ECB)模式,直接对分组明文使用伪随机置换,窃听者存在实验不安全。密码分组连接(CBC)模式,依次加密,CPA安全。输出反馈(OFB)模式,利用初始随机向量和伪随机置换生成伪随机流,F只需要为伪随机函数,CPA安全。计数器(CTR)模式,和OFB差不多,每次随机初始向量加一,F只需要为伪随机函数,CPA安全。
CCA不可区分性实验,同时可使用加密神谕机和解密神谕机。不可延展性。
分组密码
代替——置换网络。小的分组密码拼凑成大的分组密码并交换位置。不依赖密钥。S盒必须可逆,整个SP网络都是可逆的,并且是置换,SP网络有雪崩效应。
Feistel网络。S盒不必要求可逆,并且可逆,对任意选择的密钥都是置换。
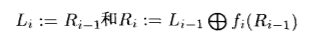
DES,16轮的Feistel网络,64位块大小,密钥长度56比特。
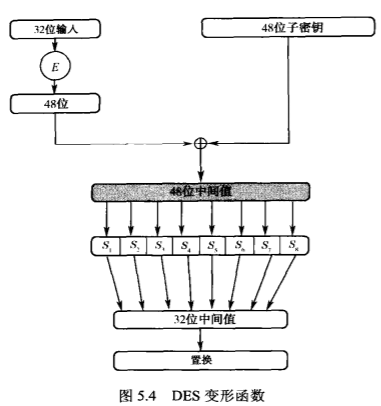
S盒的性质。

DES的改进,双重加密容易破解,三重加密有两种方式。
单向函数
求逆实验。注意只要结果映射为y就算成功。

单向函数需要对所有值域求逆都不能以多项式时间。单向置换。单向函数簇和单向置换簇。

候选的单向函数。

硬核谓词(HCP)。任意给定的谓词hc,能够证明总是存在某个单向函数f,使得hc不是该函数的硬核谓词。有硬核谓词的单射函数f必定是单向的。

消息鉴别
消息鉴别码是一个概率多项式时间算法的三元组(Gen,Mac,Vrfy)。
消息鉴别码实验,通过了则称为有在适应性选择消息攻击下的存在性不可伪造。
构造安全的消息鉴别码的证明:先证明使用真随机函数,然后替换成伪随机函数。可变长的构造。

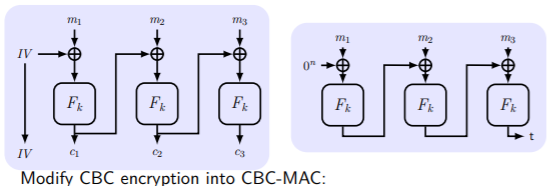
CBC-MAC。注意必须要用全0字符串作为初始向量。注意固定长度的构造只能加密固定长度的消息。不固定长度的有1.根据长度生成对应长度的密钥,2.预先考虑明文长度,3.两个密钥,第二个密钥加密第一个密钥加密后的结果。
抗碰撞散列函数。散列函数的定义。

碰撞发现实验。

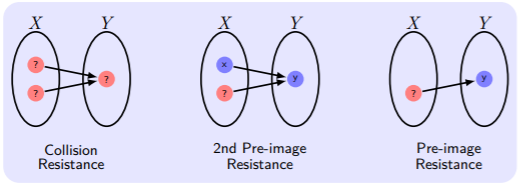
抗碰撞,抗第二原像,抗原像(包含)。
生日攻击。若散列函数能抵御在时间T内运行的碰撞寻找攻击,那么散列函数的输出长度至少应该是2logT比特。
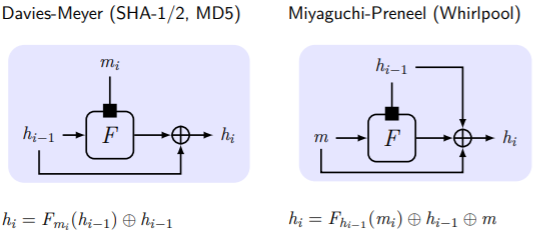
Merkle-Damgard变换。初始向量可以是任何常量代替。证明可以找出碰撞。

利用分组密码构造CRHF。
HMAC。

CCA安全和验证加密
CCA不可区分性实验。CCA安全。证明1.证明Pr[VQ]是可忽略的,2.证明没有VQ并且实验成功的概率小于等于1/2加上可忽略函数。MAC方案要求对每个k都有唯一的标记,对于每一个m都有唯一的t。

消息传输方案。

安全消息传输实验。通过了称为认证的通信。

A.E.,如果同时是CCA安全并且是认证的通信。
三种组合方式。1.加密和验证(鉴别),SSH,2.验证后加密,SSL,3.加密后验证,IPsec。加密和鉴别,不一定是安全的,因为可能违反私密性的要求。先鉴别后加密,不一定安全。加密后验证已经被证明是CCA安全的(满足要求),同时也是可鉴别的通信。
验证可能泄露明文,安全消息传输暗示CCA安全,但是反之不是,不同的安全目标通常使用不同的密钥。
公钥加密理论
使用KDC的密钥分配协议。Needham-Schroeder协议。Kerberos协议。
公钥加密,数字签名,交换式密钥交换。

公钥加密方案是一个概率多项式时间算法(Gen,Enc,Dec)。

窃听不可区分实验,给予了敌手公钥,再让敌手选择明文,相当于CPA不可区分实验,相当于多重消息加密安全。因此在窃听者存在的情况下,没有一种确定性的公钥加密方案具有不可区分加密。给定任意一个输入为定长消息的公钥加密按方案,如果是窃听者存在情况下的不可区分加密,那么可以得到输入为任意长度消息的公钥加密方案。
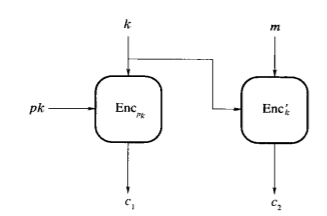
混合加密。可以加速长消息的加密和解密。其中公钥加密方案是CPA安全的,私钥加密方案是窃听者存在安全的,那么混合加密方案是CPA安全的公钥加密方案。
陷门置换簇(Gen,Samp,f,Inv)。有td就可以容易求出x。

利用陷门置换构造公钥加密方案,注意公钥加密方案中明文都可以只有1个比特。证明规约一个针对公钥加密的敌手到一个对硬核谓词的区分器。

CCA不可区分实验。

RSA
教科书式RSA。e,d的长度都是n。

GenRSA。
RSA假设。其中x相当于密文。可以根据RSA构造陷门置换。

对教科书式RSA的攻击。1.使用小e加密短消息,当使用小e时的一般攻击,2.恢复明文m的平方改进,尝试m的每个可能值。还有公共模攻击1,即N一样,e,d不一样,对内无法保密,公共模攻击2,对外无法保密。不是CCA安全的。

填充RSA。l(n)不能太大(如l(n)=2n-O(logn)),否则可以用蛮力搜索枚举所有的随机值。当RSA假设成立,l(n)=O(logn),构造方案有CPA安全。修订后的新的方案叫做OAEP(最优非对称加密充填),F-OAEP是CCA安全,F是指一个任意的陷门置换,RSA-SAEP+是CCA安全的。对RSA的攻击有Timing attack,Power attack,Defense:Blinding,Key generation trouble,Faults attack有防御Defense:check output(10%性能)。

DH问题和Elgamal加密方案
循环群。离散对数,生成元的指数。求解离散对数的算法:暴力搜索,BSGS,Pohlig-Hellman,Index calculus,general number field sieve(最好的)。离散对数实验。

DH假设。Computational Diffie-Hellman problem(CDH),decisional Diffied-Hellman problem(DDH)。DDH比CDH和DL都简单。密钥交换实验。

Diffie-Hellman密钥交换协议。概率多项式时间算法输出一个循环群,群的阶为q(||q||=n),生成元为g。无法防住中间人攻击。如果DDH是困难的,则Diffie-Hellman密钥交换协议在窃听者存在情况下是安全的。证明可以从b=0和b=1,然后转化为判定行Diffie-Hellman问题。多方密钥交换。

EIGamal加密方案。如果DDH问题相对于概率多项式时间的算法来说是困难的,则EIGamal加密方案在CPA情况下有不可区分的加密。可以共享公共参数(G,q,g)。

数字签名
与消息鉴别码的比较,发送者需要与多个接收方通信时,使用数字签名,简化密钥管理,避免为每一个密钥计算MAC标签,数字签名可以公开验证,是可传递的,具有不可抵赖性。数字签名不是公钥加密的逆向过程。
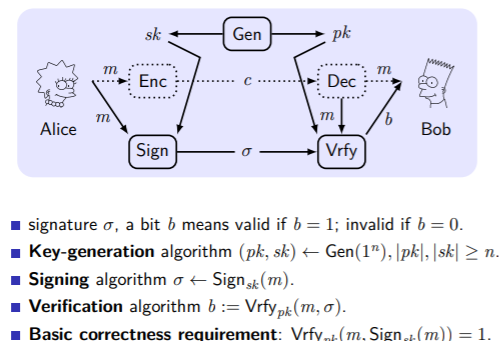
签名安全实验。通过了则称为适应性选择消息攻击下是存在性不可伪造的。

教科书式RSA签名。不安全。1.无消息攻击,利用公钥即可伪造签名。2.对任意消息伪造签名,需要得到两条同一签名者的签名。

散列后的RSA签名方案。也有无消息攻击和对任意消息伪造签名攻击。

散列后RSA为混合结构,相对教科书式RSA有另一个优势,可以用于对任意长度的比特串进行签名。如果构造用的公钥数字签名方案是适应性选择消息攻击下的存在性不可伪造的,且散列函数是抗碰撞的,那么构造方案在适应性选择消息攻击下是存在性不可伪造的。

离散对数的数字签名。认证方案的定义。

Fiat-Shamir变换,可以构造一个(非交互的)签名方案,通过签名方自己运行协议。如果认证方案是安全的认证方案并且H是随机预言机,那么Fiat-Shamir变换得到一个安全的签名方案。

Schnorr认证方案。如果离散对数问题是困难的,那么Schnorr认证方案是安全的。
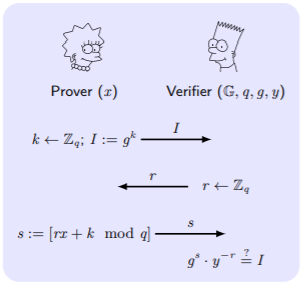
Schnorr签名方案。DSS(数字签名标准)使用DSA(数字签名算法),DSA是一种EIGamal签名方案的变体)。

一次性签名方案。当此方案只用于对一个消息进行签名时,是安全的。一次性签名实验。通过一次性签名实验称为签名方案在单消息攻击下是存在性不可伪造的,或者为一次性签名方案。具体有Lamport签名方案。

Lamport签名方案。设l为任意多项式,如果f为单向函数,则构造方案为一个消息长度为l的一次性签名方案。如果存在单向函数,则对于任意多项式l,都存在一个针对消息长度为l的一次性签名方案。

适应性选择消息攻击下存在性不可伪造的签名方案有:1.基于Chain的签名,2.基于Tree的签名。
数字证书和公钥基础设施。单一认证机构。多个证书认证机构。授权和证书链。信任Web模型。吊销证书,过期,撤销,都可以通过添加额外信息。